OBSERVING PRIMARY DIRECTIONS IN ASTROMAPPING

Introduction

Astromapping techniques (AstroCartoGraphy, Local Space, Geodetic Astrology, and CycloCartoGraphy) are methods that examine how the planets in a natal chart manifest across the surface of the Earth. These systems typically project the natal chart onto geographical space, yet they can also be correlated with the temporal cycles in a person’s life. For this reason, combining astrology’s time-based methods (such as Primary Directions) with spatial techniques can offer astrologers both a temporal and spatial perspective.

Historical Background

Primary Direction is one of the oldest known timing techniques in astrology and holds a central position in Hellenistic, Medieval, and Renaissance traditions. Although many modern astrologers know this technique primarily through Ptolemy, it in fact developed within a much older lineage.

At the foundation of Primary Directions lies the rotation of the Earth on its axis. Because the Earth rotates from west to east, the sky appears to move from east to west. This motion represents the full rotation of the celestial sphere within 24 hours.

Ancient astrologers regarded this 24-hour rotation as a model of human life. The sky’s 360° rotation in one day symbolically represents an entire lifetime. Thus:

The rotation of 1° of the celestial sphere = 1 year of life

5′ = 1 month

1′ = 6 days

What progresses in this technique is not the planets themselves, but the way the Earth’s rotation brings indicators in the chart into contact with each other.

In Primary Directions, what we measure is the angular approach between the significator and the promissor and convert this angular distance into a time period. Therefore, PD is not planetary motion; it is the timing of axial movement and symbolic contact.

Hellenistic astrologers, Thrasyllus (1st c. BCE), Dorotheus (c. 75 CE), Vettius Valens (2nd c. CE) were among the first to clearly define the principle of directing. In particular, the examples in Valens’ Anthologiae that employ “astronomical hour-angles” demonstrate that this technique was already widely used in the Hellenistic period.

Thereafter:

         Ptolemy (2nd c. CE): Systematically defines Primary Directions; time key is 1° = 1 year.

         Porphyry (3rd c. CE): Elaborates the relationships between the meridian and oblique ascensions.

         Medieval astrologers (Arabic translations of Dorotheus, Sahl, Masha’allah, Abu Ma‘shar, Alcabitius, Bonatti): Develop the technique using RA (Right Ascension), OA (Oblique Ascension), and semi-arc models.

This tradition reaches its peak during the Renaissance:

         Regiomontanus (1436–1476) - Circle of Position Method

         Jerome Cardano (1501–1576) - Time key: 59′12″

         Valentine Naibod (1523–1593) - Time key: 59′08″

  Placido de Titis (1603–1668) - Semi-Arc model; becomes the most influential system underlying modern ephemeris-based directing

  Jean-Baptiste Morin (1583–1656) - Astrologia Gallica is considered the most detailed 17th-century work explaining both the mathematics and philosophy of Primary Directions. For Morin, PD is the main technique that determines both the cause and timing of events. His semi-arc model forms the basis of the system now known as Morinus Primary Directions, used in many modern programs.

These figures together form the foundation of all Primary Direction systems used today. Though their methods differ, they share one essential principle.

Figure 1 - The Vernal Equinox: the intersection point of the ecliptic and the celestial equator, defines the origin of the Right Ascension system. The equatorial arc measured along the celestial equator forms the basis of symbolic time within Primary Directions.

The foundation of the Primary Directions technique lies in Earth’s daily rotation around its axis. Earth completes one full rotation in approximately 24 hours, and in astronomical terms this motion corresponds to a 360° rotation projected onto the celestial equator. This rotation is converted into the Right Ascension (RA) scale, which is measured along the celestial equator. RA begins at the Vernal Equinox (the point where the ecliptic intersects the celestial equator) and is expressed in hours from 0h to 24h; this intersection represents the zero reference of the equatorial coordinate system.

The position of a celestial body (or an angular point) along the equator is expressed as an equatorial arc measured from the Vernal Equinox. This arc serves as the symbolic counterpart of the Sun’s apparent annual motion across the sky: Earth’s daily rotation is rescaled within the astrological time framework so that the motion along the equator corresponds to years in the native’s life. In other words, the angular separation on the celestial equator is transformed into a symbolic temporal interval that represents a specific phase of life.

As illustrated in Figure 1, the Vernal Equinox simultaneously links two fundamental systems:

— The ecliptic, representing the Sun’s annual path

— The celestial equator, representing Earth’s axial rotation

This intersection point constitutes the beginning of the RA system. Each hour of RA corresponds to approximately 15° of equatorial arc, determined by Earth’s rotation. The time keys used in Primary Directions are based on this symbolic progression along the equator: the equatorial distance between a significator and its promissor is converted into a specific span of years in a person’s life.

For this reason, Primary Directions do not operate with the literal positions of celestial bodies, but rather with their temporal projections onto the equatorial plane. The symbolic transformation of Earth’s axial motion into time is the foundation of both the Placidus semi-arc system and the Ptolemaic time key. Thus, angular separations in the sky become directional indicators corresponding to distinct periods within the life cycle.

Comparison with Other Predictive Techniques

Astrological timing methods can be divided into two general categories: real-motion (astronomical) techniques and equivalence-based (analogical) techniques. This distinction was emphasized particularly by Medieval and Renaissance astrologers.

Category	Techniques
Real-Motion (Astronomical)	Transits, Planetary Returns (Solar/Lunar Returns), Primary Directions
Analogical (Equivalence-Based)	Secondary Progressions (Tertiary etc.)Profections (Time Lord techniques)Planetary Arcs (Solar / Lunar Arc etc.)

1. Real-Motion Techniques (Astronomical)

The common feature of these techniques is that they are based on actual celestial motions. The planets’ movement along the ecliptic, the Earth’s rotation around its axis, the Moon’s orbital cycle, or the Sun’s precessional cycle are used directly. For this reason, these methods strongly describe external events, physical circumstances, and concrete developments in a person’s life.

a. Transits: In this group, we may first consider transits. Transits represent the real-time astronomical movements in the sky, and we project these values into charts using our coordinate systems. In fact, every chart is a transit chart. For instance, a natal chart is simply the transit chart of the sky on the day of birth. Here, ecliptic longitude, declination, and retrograde motion are entirely real.

b. Planetary Returns: Solar, Lunar, or other planetary returns are also essentially transit charts. The only difference is that we take as reference the exact degree and minute at which the planet returns to its natal position, and at that moment, we examine the chart using the actual current sky transits. For example, the solar return is based on the Earth’s true orbital motion around the Sun. Likewise, the lunar return is based on the Moon’s actual revolution along the ecliptic. The Moon’s mean synodic period is 29.53 days, and every return chart is calculated using its real astronomical position.(Note: This is why in modern astrology there is a debate between precession-corrected and non-precessed solar returns.)

c. Primary Directions: They are entirely based on the Earth’s rotation. Here we use real astronomical concepts such as RA (Right Ascension), OA (Oblique Ascension), meridian distance, Semi-arc (SDA), Ascensional Difference (AD). We convert the planets’ apparent 24-hour motion into symbolic years.

2. Equivalence-Based (Analogical) Techniques (Harmonic Adjustment)

These methods are not based on real celestial motion; symbolic speeds are assigned to planets and angles. This structure is actually hidden within fractal knowledge, because the part must contain the whole, and the whole must contain the part. Therefore, when our view of time becomes symbolic, we can scale it according to the reference framework we choose.

a. Secondary Progressions: In this technique, we apply the rule “1 day = 1 year,” but this application is based on a part-to-whole relationship. The actual observation is the movement of the planets during one day of transits, but translating that one day as one year is a timing correspondence. In reality, no celestial body moves to its “30-day position” when a person turns 30.

b. Tertiary Progressions: In this technique, different fractal scales such as “1 day = 1 month” are used. For example:Tertiary I: 1 day -> 1 monthTertiary II: 1 day -> 1 weekHere we adapt the part-whole relationship to the time scale. This is entirely analogical and has no astronomical basis.

c. Profections: Profection is a completely analogical method. Each of the 12 houses in the natal chart represents one year; the individual advances to the next house every year. The same logic can be applied to smaller time scales: one year is divided into 12 months, and thus the active house for the year is divided into 12 subsections. Since a month of approximately 30 days ≈ 12 parts is assumed, each part corresponds to about 2.5 days.The fundamental logic of profection is the principle of “scaling the whole into parts and adapting the part back into the whole.”

d. Progressions by Planetary Arcs: In arc-based progressions, we first choose a reference point (e.g., planets, ASC, MC, Vertex, North Node, Lots, or any sensitive point). The arc traveled by this reference point up to a specific date is calculated. This arc may be measured using Ecliptic longitude (λ), Right Ascension (RA), equatorial coordinates, or MC/ASC arcs (meridian arcs).Which coordinate system is used depends on the technique itself. After the arc is determined, this arc is applied equally to all indicators in the chart. Thus, the chart undergoes a symbolic transformation synchronized with the progression of the reference point. Solar Arc is the simplest example. The arc travelled by the Sun is applied to all points. However: Solar Arc motion has no astronomical counterpart; it is a symbolic technique based entirely on the principle of equivalence.

AstroMapping: The Geographical Reflection of the Natal Chart + Timing Techniques

At the core of astrocartography lies the projection of a planet’s true astronomical position at a given moment onto the Earth. Software calculates the angular positions of the planets (that is, on which latitude/longitude line of the chart they are rising, culminating, setting, or at the lower meridian, in classical terms, their relationship with ASC, MC, DSC, and IC) and plots them on a world map using different types of projection.

Depending on the mode we use (for example, zodiacal or mundo drawings, gnomonic or other projections), the tilt and shape of the lines may change; however, they all share one common feature: The angular relationship a planet forms with the horizon and meridian at a given moment creates a specific projection on the Earth.

In AstroMapping applications, our aim is to see this geographical projection of the birth moment. But beyond that, we also want to examine which regions resonate with the celestial themes activated throughout the person’s life by different timing techniques (transits, return charts, progressions, etc.). For this reason, we use cartographic projections of the charts we cast with different predictive techniques, and in this way we can read both time and space together.

The critical point here is this:

The progressed techniques used in AstroMapping do not create a new “type of chart.” In other words, we do not calculate a new “ASC–MC line” in cartography. Instead, we advance the chart to the chosen time, and then project this progressed chart and read it. In this way, we project the time-advanced chart onto space.

This approach is fully accepted in CCG. For example, the Secondary Progressed chart describes the person’s inner, psychological time, and it is possible to project this onto the spatial plane. The Solar Arc chart shows the person’s general direction and long-term themes, and this also has a spatial counterpart. Tertiary Progressions provide micro-cycles and can be used for small-scale spatial sensitivities.

For AstroMapping to work, a chart must produce a real set of coordinates for the planets and the angles. These coordinates are:

         Ecliptic longitude (λ)

         Equatorial coordinates: RA (Right Ascension) and declination

         The relationship of the local meridian and horizon (the ability to calculate ASC/MC)

If a chart satisfies these three conditions, it can be projected onto the world. For this reason, some progression techniques can be used in cartography, while others cannot. For example, Secondary progressions or Solar Arc cartography produce RA, declination, and ecliptic longitude just like a normal chart. The planets advance to a new degree. In fact, Solar Arc adds a fixed arc in ecliptic longitude, so the declination and RA coordinates of all planets can be calculated. Planetary return charts are already real astronomical charts anyway. We can use them in cartography as transits, or treat them as progressed moments. Profections, on the other hand, cannot produce these values, so they appear to be outside the scope of cartography; however, through this method we can still obtain time lords and of course work with the cartographic projections of their indicators.

When we come to the technique of Primary Directions, things are somewhat different.

Unlike other progression methods, Primary Directions do not produce a new celestial position. When we cast Secondary, Solar Arc, or Tertiary charts, the program calculates a new ecliptic longitude, a new right ascension, and a new declination for each planet; this allows them to be projected onto the Earth just like natal or transit charts. In Primary Directions, however, no such chart is produced. What Primary Directions provide is not a new sky, but only a directed arc; when we convert this arc into age, what we are left with is merely a time marker for a specific moment. In classical language, this is “the moment when the significator directs toward the promissor”; yet at that moment the planets are not in new positions, only their geometric relationships are symbolically considered to have completed.

Therefore, since there is no new celestial position that can be projected onto the Earth, Primary Directions have no direct cartographic map. This is precisely why software cannot give us a chart when we click on the “time of aspect formation” in the Primary Directions list. As the program cannot generate a new sky, it only opens the transit chart for that day; however, that transit chart is not the Primary Direction itself.

Because of all this, Primary Directions are a powerful timing tool in astrology, but they are a method without a spatial counterpart. Even so, it is still possible to speak of an indirect contribution of Primary Directions to cartography.

The symbolic moment determined by PD indicates one of the important threshold periods in the person’s life, and we can project the transit chart of this moment onto the geographical plane to examine the spatial projection of the process. In this way, we do not interpret the primary direction itself in cartography, but rather the transits of the period it triggers. This indirect approach is necessary by the very nature of Primary Directions, because although they do not create a chart, they tell us at which moment the chart activates which theme.

Consequently, the relationship between Primary Directions and AstroMapping is not direct, but established through temporal mediation. Unlike techniques such as Secondary Progressions or Solar Arc that “produce charts,” Primary Directions give us only a moment; and the sky of that moment (the transits) is the only data that can be spatially projected.

Now let us show how this distinction can be observed in practical application with example charts, and examine in detail how PD can be read on the geographical plane in an indirect yet meaningful way.

CASE STUDY: An Experience of Losing a Sibling

Mr. Client – technical observation only, without birth data

One of the PD triggers frequently encountered in astrological work is planets directed toward the angles. In this method, significant events that befall a person can often be observed functionally. They can be read more as fate-related developments. In this example, we will examine an event involving death.

In this case study, the ruler of the person’s 3rd house (house of siblings – Libra) is Venus. Venus is at 11° Scorpio in the natal chart, and the IC is at 5°52’ Scorpio. In other words, at birth there is a distance of approximately 5 degrees between Venus and the IC.

Even though this closeness in ecliptic longitude already draws attention, what is critical from the standpoint of Primary Directions is the difference in Right Ascension (RA) and declination between these two points.

In this case, the coordinates of Venus, ruler of the 3rd house, are given as:

RA = 218°10’, declination = –16°20’.

The coordinates of the IC are:

RA = 213°33’, declination = –13°28’.

These data show that at birth, Venus is approximately 4°37’ ahead of the IC in RA.

Considering Ptolemy’s key of 1° = 1 year, this difference corresponds to a symbolic arc of about 4.6 years. However, in Primary Directions, taking only the RA difference is not sufficient; when the semi-arc of the planet, the effect of its declination, and latitude corrections are taken into account, the exact direction time that appears often yields an age several years later than the simple RA difference.

In this case, the Primary Direction calculation shows that the symbolic time at which Venus directs to the IC corresponds to the period of the native’s post-adolescent young adulthood. This date coincides with a deep breaking point in the person’s life, specifically a heavy event related to the themes of “family roots – siblings – home.” Records show that during this period, the native experienced the loss of a sibling.

When a planet or angle is close to a point in the natal chart, Primary Directions will direct that planet toward that point based on the Earth’s rotation. When this direction completes, a threshold emerges that classical texts define as a “turning point in life.” Here, Venus directing to the IC produced meaningful timing both thematically (ruler of the sibling house + roots/IC) and experientially (a family loss).

It should be emphasized that Primary Directions do not produce a new chart; therefore, the direction itself has no cartographic line. However, the exact date determined by PD offers a powerful anchor for examining the transit chart of that period, and the cartography of that transit chart.

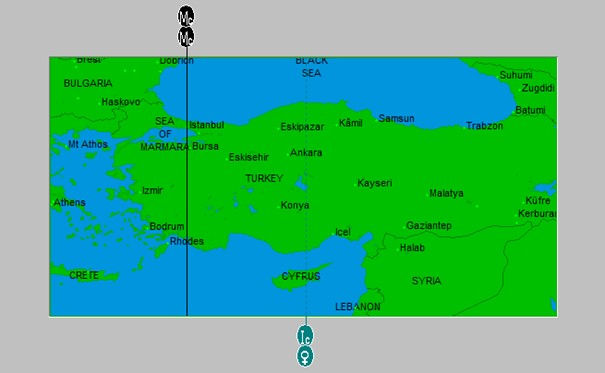
When we open the natal chart in cartography, because the person is born in Istanbul, the ASC and MC lines will be located there. The Venus–IC line, however, passes east of Istanbul, through the Çankırı–Ankara region. There is approximately a 3.5° longitude difference between the two lines.

This difference parallels the RA difference obtained in the PD calculation. In both cases, Venus is “approaching” the IC but has not yet fully conjoined it. In other words, the spatial map gives us the positional projection of the PD mathematics at birth.

According to Ptolemy’s time key, 1° of arc corresponds to 1 year, so the 4°37’ difference represents approximately 4.6 years of directional motion. When we convert this same difference into hours, we see a similar relationship: along the celestial equator, a 1° difference in RA corresponds to roughly 4 minutes of time. Therefore, 4°37’ corresponds to about 18–19 minutes of birth time deviation. This may be summarized as:

4°37’ RA ≈ 4.6 years (according to Ptolemy’s key)

4°37’ RA ≈ 18–19 minutes (according to Earth’s rotation rate)

This is where the critical observation in the case becomes relevant. Approximately 20 minutes after the recorded birth time, Venus is exactly conjunct the IC in the natal chart. The 18–19-minute time span derived from the RA difference in PD corresponds to the same geometric reality as the 20-minute difference observed in the transit: one expresses this difference in years in Primary Directions, the other expresses the same difference in minutes at the transit level.

This relationship is also observable in cartography. As mentioned earlier, when the natal cartography is opened, the Venus–IC line passes slightly east of Istanbul, close to the Çankırı–Ankara region. The longitude difference of approximately 3.5° between the birthplace and the Venus–IC line corresponds to roughly a 14-minute local time shift when we consider that 1° of longitude on Earth corresponds to approximately 4 minutes of time. This points to a correction within the same scale as the 18–19-minute value derived from the RA difference. In other words, the Venus–IC line lies slightly east of Istanbul at the moment of birth, but as time progresses (as the Earth rotates), this line moves toward Istanbul.

Here we also observe that the movement occurs from right to left. In truth, we are roughly calculating the distance between the natal line and the person’s birthplace. When we concretize this at the transit level, the picture becomes even clearer. When the transit chart for the moment when the transit IC makes an exact conjunction with natal Venus (natal time +20 minutes) is opened in cartography, we see that the Venus–IC line now passes through Istanbul. The line that previously ran through Çankırı–Ankara in the natal chart shifts onto Istanbul at the transit moment.

What is being done here is observing the angular difference given by Primary Directions both in the time plane (in years and minutes) and in the spatial plane (in longitude difference and line shift). The Primary Direction itself still does not produce a new chart; yet the geometric difference underlying the direction becomes clearly visible in cartography at the moment transit IC meets natal Venus.

This example shows that although Primary Directions do not create a direct cartographic line, the directional arc they produce is fed by the same geometric relationship in both time and space, and that this relationship can be observed indirectly but quite meaningfully through transit cartography.

CASE STUDY 2: Determining the Time of Marriage

Ms. Client – technical demonstration based on 06:49 birth time

In this case study, the person was born with Capricorn rising. In the chart, the 7th house (marriage–partner house) begins in Cancer, and its ruler is the Moon. Therefore, the Moon’s position in the chart and especially its potential primary directions to the angles are critically important at major turning points in life, such as marriage.

In the previous example, the primary directions were calculated through the MC/IC axis using only the difference in Right Ascension (RA). Because the MC is defined directly on the celestial equator, the relationship between RA difference and symbolic time in the Ptolemaic model remains clear and straightforward. In the present example, however, we work through the ASC–DSC axis.

Notice that this time we are not directing the planet toward the ASC but directing the Ascendant toward the planet.

Since the ASC is determined by the horizon and the observer’s latitude, the calculation changes substantially; oblique ascension, ascensional difference, and especially the semi-diurnal arc must be included.

To begin, we summarize the equatorial data from the natal chart needed for the computation:

Birthplace: Istanbul (φ ≈ 41° N latitude)

Birth time: 06:49

Local Sidereal Time (LST): 13h 43m 55s -> ≈ 205.98°

Moon’s equatorial coordinates:

RA(Moon) = 249°29′δ(Moon) = −27°14′

Ascendant’s equatorial coordinates:

RA(ASC) = 273°52′δ(ASC) = −23°23′

Using these data, we can compute the primary direction of the Ascendant toward the Moon step by step according to the Placidus semi-arc method.

STEP I:

The first, rough approach is simply to compare their RA values:

RA(ASC) − RA(Moon) = 273°52′ − 249°29′ ≈ 24°23′.

With the Ptolemaic key, where 1° ≈ 1 year, this yields a symbolic arc of approximately 24.4 years. This is usually sufficient for MC/IC directions, since the MC lies on the equator. For the Ascendant, however, this approximation is overly optimistic because it ignores the effects of the horizon and latitude. We now recompute the same relation using the actual semi-arc geometry, that is, by incorporating the horizon–latitude framework.

STEP II:

In the Placidus system, the semi-diurnal arc (S) of a point is half of its diurnal rotation between the horizon and the meridian. On the equatorial plane it is computed as cos S = −tan φ · tan δ. Using Istanbul’s latitude (φ ≈ 41°):

Moon: δ = −27°14′ -> S(Moon) ≈ 63.4°

Ascendant: δ = −23°23′ -> S(ASC) ≈ 67.9°

These values show that the Moon’s path between horizon and meridian is slightly shorter than that of the Ascendant.

STEP III:

The position of each point with respect to the meridian is expressed by its hour angle

(H): H = LST − RA. With LST ≈ 205.98°

H(Moon) = 205.98° − 249.48° ≈ −43.5°

H(ASC) = 205.98° − 273.87° ≈ −67.9°

The negative sign indicates that both points lie east of the meridian and have not yet culminated.

STEP IV:

In the Placidus semi-arc method, the direction is determined by the mundo position of each point. The mundo position can be expressed as q = H / S. For the direct direction of the ASC toward the Moon, the advanced position of the Ascendant (H′ASC) must match the mundo position of the Moon: q′ASC = qMoon.

This gives:

(H'ASC + E) / S'ASC = H'Moon / S'Moon

where E is the equatorial arc required to direct the Ascendant.

Solving for E:

E = (H'Moon · S'ASC / S'Moon) − H'ASC

Substituting the numerical values:

H'Moon ≈ −43.5°

H'ASC ≈ −67.9°

S'Moon ≈ 63.4°

S'ASC ≈ 67.9°

gives E ≈ 21.3°. This is the true equatorial arc necessary for the mundo conjunction of the ASC with the Moon.

STEP V:

Using the Ptolemaic time key (1° ≈ 1 year), an arc of E ≈ 21.3° corresponds to roughly 21.3 years. The key point is this: whereas the simple RA difference suggested 24.4 years, incorporating the effects of the horizon and latitude through the semi-arc calculation yields 21.3 years. In MC/IC directions, this discrepancy is usually minimal, but in ASC/DSC directions oblique ascension and ascensional difference can introduce several years of divergence. This example makes clear that the semi-arc method is essential whenever the Ascendant axis is involved.

The resulting timing is also meaningful, as it corresponds to the period in which the first steps toward marriage were taken. The native met the future spouse around this time. Thus, the direction does not signify the exact year of marriage but rather the onset of the sequence of events that led to it. Given that a primary direction activates not only a single event but an entire thematic process, the symbolic timing obtained here is fully coherent with the lived experience.

Let us now attempt to observe these findings on the astrocartographic map. As is well known, Primary Directions do not generate a new chart in the cartographic sense; therefore, the direction itself cannot be visualized as a “cartography line.” For this reason, it is not possible to read the spatial projection of a direction directly from a PD map. Nevertheless, the temporal information produced by PD provides a strong framework for interpreting both the transit chart and the corresponding transit astrocartography.

When the transit of the day on which the Moon–ASC direction completes within the marriage year is examined, the following mechanical observation can be made: the minute at which the transit ASC reaches the natal Moon degree corresponds to a certain amount of time earlier than the person’s recorded birth time.

In this example, the natal Moon degree of 11°46’ Sagittarius is reached by the transit ASC earlier on the person’s birthday than 06:49, around 05:09.

This means: The person experienced the Moon–ASC conjunction about 1 hour and 40 minutes before their birth.

Therefore, because this conjunction did not occur at the birth moment, the Moon–ASC contact is not yet closed in the natal chart. And this is exactly what the logic of Primary Directions tells us. At the moment of birth, the Moon is behind the ASC by a certain RA difference. As the Earth rotates, the ASC approaches the Moon.

When the natal chart is opened in cartography, the Moon–ASC line is clearly positioned west of Istanbul. The reason is that at birth, the Moon is behind the ASC in terms of RA. When a planet’s RA is smaller than the horizon, its rising line passes west of the place of birth.

In this example, the Moon–ASC line extends through Italy, and there is approximately a 15° longitude difference between the birthplace and this line. Considering the rule that 1° of longitude on Earth corresponds to approximately 4 minutes of time, this longitude difference corresponds to roughly 60 minutes of local time. This indicates that the Moon–ASC contact had not yet closed at the moment of birth.

Now comes the critical observation:

When the cartography of the transit moment at 05:09 (the moment when the transit ASC reaches the natal Moon degree) is examined, it becomes evident that the Moon rising line approaches Istanbul noticeably, but does not pass directly over the birthplace.

In the natal situation: the Moon–ASC line is 15° west of Istanbul.

At the moment of transit ASC = natal Moon: the same line is 3° east of Istanbul.

This time, the Moon–ASC line is approximately 3° east of the birthplace. In other words, the line that was west of Istanbul at the natal moment has shifted to the east of Istanbul at the transit moment; thus, a spatial shift of approximately 18° has occurred between the two moments.

The primary reason for this shift is that the horizon and meridian at the transit moment are in a different position compared to the birth moment. Since the ASC’s arrival at 11°46’ Sagittarius (05:09) happens about 1 hour 40 minutes before the recorded birth time, as the Earth rotates, the horizon moves toward the Moon’s RA, but begins to distance again before aligning exactly.

Parallax is also notable here. The Moon is very close to the Earth compared to other planets, and therefore its contact lines with the horizon (rising/setting) can show several degrees of shift on the geographical plane. For this reason, Moon lines, especially ASC/DSC contacts, respond more sensitively to the horizon position at transit times.

When these two pieces of data are considered together, it becomes clear that the Moon–ASC direction arc expresses the same geometric difference both in the time plane (approximately 24 years of PD direction) and in the spatial plane (roughly an 18° longitude shift). Even though Primary Directions do not create a direct cartographic line, when the direction derived from the RA–semi-arc difference is caught at the transit moment, its spatial projection becomes clearly visible in transit cartography.

Structural Difference Between Primary Directions and AstroCartoGraphy

While the technique of Primary Directions and the AstroCartography system may often indicate similar periods in a person’s life, the astronomical reference frameworks underlying each method are fundamentally different. For this reason, a symbolic indication derived from Primary Directions does not necessarily correspond with millimetric precision to a physical line on a map. This divergence becomes especially apparent when examining directions involving the Ascendant and Descendant. The reasons for this difference can be understood more clearly when the accompanying figures are considered.

Figure 2 - The MC/IC axis is defined by the intersection of the ecliptic and the local meridian. Because this point lies directly on the equatorial framework, MC directions correspond closely with equatorial arcs in Primary Directions.

As seen in the diagram, the MC is defined at the intersection of the observer’s meridian and the ecliptic. The meridian is a fixed great circle of the celestial sphere and stands in a direct right-angle relationship with the celestial equator. Consequently, the position of the MC can be measured directly in Right Ascension (RA) within the equatorial coordinate system. Since Primary Directions are based on equatorial arcs, the MC aligns naturally with the geometry of this system. For this reason, directions involving the MC/IC axis typically yield results that correspond more closely with the actual MC lines on an AstroCartoGraphy map and tend to show very small margins of deviation.

Figure 3 - The ASC/DSC axis emerges from the intersection of the ecliptic, celestial equator, and local horizon. Its geometry depends on latitude, making ASC directions less directly aligned with equatorial arcs and more prone to spatial deviation on AstroCartoGraphy.

The third figure illustrates the definition of the ASC–DSC axis. This diagram shows how the ecliptic (orange), the celestial equator (blue), and the horizon (green) form three inclined planes intersecting at different angles upon the celestial sphere. The ASC is produced from the intersection of these three planes; in contrast to the MC, it is not defined by a single, stable geometric relation. Because the horizon depends on the observer’s latitude, the RA value corresponding to the Ascendant’s position on the celestial equator cannot be measured directly. Instead, oblique ascension, ascensional difference, and conversions related to latitude and obliquity must be employed.

This multi-layered chain of transformations introduces a natural separation between Primary Directions, which operate on pure equatorial geometry, and AstroCartoGraphy, which is based on ecliptic projection. As a result, ASC/DSC directions cannot fully conform to the equatorial arc principle of PD; while their symbolic timing often remains consistent, their physical location on the map cannot be expected to coincide with exact precision.

Evaluating these two diagrams together makes clear why Primary Directions work more coherently and consistently with the MC–IC axis, whereas ASC–DSC directions require a broader tolerance range. The MC is defined solely through the meridian and the equator, harmonizing directly with RA differences used in PD calculations. The Ascendant, however, is influenced by the combined geometry of the ecliptic, equator, and horizon. When compared with ACG lines, it is therefore expected to show measurable displacement. These discrepancies arise not from any computational error, but from the inherently different astronomical reference systems upon which each method is built. It is therefore observationally evident that ASC/DSC directions may show correct symbolic timing even when they do not physically intersect the same geographical point.

Conclusion

When applied with the Ptolemaic time key and the Placidus semi-arc method, Primary Directions are grounded entirely in the equatorial reference system. Each arc used in the computation is a symbolic temporal progression derived from Earth’s rotation, defined through equal hour angles rather than ecliptic degrees. The equatorial arc expresses how far a planet or angle is “directed,” and this arc is directly connected to the symbolic transformation of rotational movement into time. Thus, results obtained through Primary Directions do not represent the physical positions of the planets in the sky, but rather a symbolic transformation of the time–space relationship.

AstroCartoGraphy maps, by contrast, rely on an entirely different computational framework. These maps display the geographical meridian on which a planet is rising, setting, culminating, or anti-culminating at a specific moment in time. They are based on real astronomical quantities: Local Sidereal Time, latitude (φ), longitude (λ), Earth’s obliquity (ε), and the instantaneous declination (δ) of celestial bodies. Each planetary line on an ACG map is the product of projecting these real astronomical relationships onto the surface of the Earth. AstroCartoGraphy lines are therefore concrete, measurable paths rooted in the actual rotation of the Earth.

From this perspective, the difference in outcomes between the two systems becomes unavoidable. The Ascendant’s reaching the Moon through Primary Directions is a symbolic temporal contact; it cannot be expected to guarantee that, at the corresponding date, the same Ascendant degree will rise over the same geographic location. The Ascendant’s rising position is affected by latitude, declination, obliquity, semi-diurnal arcs, and oblique ascension calculations. Even if an Ascendant degree rose in Istanbul at the native’s birth, the same degree may rise over a different meridian during the transit due to shifts in Earth’s rotation, precession, and latitude/obliquity effects.

This discrepancy becomes even more pronounced when dealing with the Moon, whose high parallax, rapid motion, variable declination, and distance from the Earth produce significant horizon-related distortions. These factors make it impossible to align the Moon’s relationship with the horizon through RA-based measurement alone. Consequently, when a Moon–ASC direction is derived through RA-based computation, it will not produce the same linear relationship between time and geographic location that one might expect from a simpler MC direction.

The MC and IC axes behave far more simply. The MC is determined entirely by the Right Ascension of the meridian and is directly tied to geographic longitude. Therefore, MC/IC directions show much clearer correspondence between Primary Directions and AstroCartoGraphy lines. The Ascendant, however, is governed by oblique geometry involving declination, latitude, obliquity, semi-diurnal arcs (S), hour angles (H), oblique ascension (OA), and ascensional difference (AD). Because the rising point is inherently “tilted,” the same Ascendant degree may cross a different geographical corridor in transit.

This divergence does not result from any flaw in the technique but from the fundamental nature of the systems themselves. Primary Directions produce symbolic equatorial arcs; AstroCartoGraphy maps project real astronomical rising lines onto the globe. It is therefore entirely normal for ASC lines in transit not to coincide with the natal city. In such cases, the lines represent not an exact point but an “influence corridor.” Jim Lewis himself described AstroCartoGraphy lines as “lines,” “corridors,” or “zones of influence,” noting that ASC and DSC lines in particular may shift several degrees east or west across Earth’s surface.

In short, the fact that a Primary Direction does not pass through the exact coordinates of the natal city does not indicate a contradiction between the two methods. An ASC line falling 100–300 km east or west of the natal location during a transit is completely normal. The inability of the Ascendant degree to pass through the same geographical point at the corresponding time does not weaken the validity of Primary Directions; rather, it reveals the different reference frameworks upon which the two techniques operate.

Thus, the astrological value of Primary Directions remains intact at both theoretical and practical levels. Yet from the perspective of spatial techniques, it becomes clear that the arc of a primary direction cannot be projected directly onto the globe. PD determines the time; the spatial correspondence of that time must be observed through the transit chart’s cartographic projection. In this sense, PD sets the temporal orientation, the transit describes the astronomical state, and AstroCartoGraphy situates that state in space.

As demonstrated in this study, Primary Directions continue to stand as one of astrology’s most refined timing techniques. When integrated with modern astro-mapping practices, they can be used not as direct spatial tools but as temporal anchors, preserving the depth of classical astrology while forming a coherent synthesis with contemporary locational methods.

Kenan Yasin Bölükbaşı

25.11.2025, 09:31, Istanbul

Founder DAA, ISAR Cap, council APAI, AA Member and C*I*A Eu Representative

REFERENCES

Classical

Ptolemy, Tetrabiblos

Dorotheus of Sidon, Carmen Astrologicum

Paulus Alexandrinus, Introductory Matters

Abu Ma‘shar, Abbreviation of the Introduction to Astrology

Al-Biruni, Kitab al-Tafhim

Māshā’allāh, De Revolutionibus Nativitatum

Regiomontanus, Tabulae Directionum

Placidus de Titis, Physiomathematica

Jean-Baptiste Morin, Astrologia Gallica

Modern

W. J. Simmonite, Arcana of Astrology (2003 reprint)

Llewellyn George, A to Z Horoscope Maker and Delineator (1910)

Martin Gansten, Primary Directions: Astrology’s Old Master Technique

Martin Gansten, “Primary Directions in Classical Astrology” (Journal Articles)

Jim Lewis, “The Psychology of AstroCartGraphy.”

Martin Davis, “Astrolocality in Astrology”

Kenan Yasin, “Deneysel Astroloji Akademi Advanced Course Notes”

Kenan Yasin, “Kepler Collage CCG Training Notes”

APPENDICES

APPENDIX 1 - Glossary of Abbreviations

RA: Right Ascension

OA: Oblique Ascension

AD: Ascensional Difference

MD: Meridian Distance

SDA: Semi-Arc

PD: Primary Directions

SR: Solar Return

LR: Lunar Return

APPENDIX 2 - Comparative Table of RA and OA Calculations

Concept	Definition	Plane Used	Area of Application
RA - Right Ascension	Longitude measured 0°–360° on the celestial equator from the Vernal Point	Equatorial	MC–IC–based PD directions, meridian calculations
OA - Oblique Ascension	The equatorial equivalent of a point’s rising on the local horizon	Horizon–Ecliptic	ASC–DSC–based directions, latitude corrections
Declination (δ)	North–south angular distance from the celestial equator	Equatorial	RA/OA conversions
Ascensional Difference (AD)	Correction value determining the RA–OA difference	Latitude–Declination	All ASC-based PD calculations
Meridian Distance (MD)	RA distance of a point from the MC/IC	Equatorial	Root calculation of MC–IC directions

Copyright Notice

All rights to this article are reserved by Kenan Yasin Bölükbaşı.

Unauthorized copying, distribution, or sharing of the content on online platforms is strictly prohibited. © 2025 – Kenan Yasin, Deneysel Astroloji Akademi.